
A early generation Radio Shack Color Computer not too different from my old machine.
More than a few years ago, I was blessed to acquire a Radio Shack Color Computer which was brand new and with which I first explored the world of computing LONG before there was an Internet to connect to.
Back then, we haunted the BASIC language books and BBS systems as well as user meetings to share code and ideas. It was a different era where information was much harder to acquire than today and we scoured periodicals written in ACTUAL PRINT on paper rather than to just visit web sites like we do today to get our information fixes.
I remember one night coming home from work and watched the following PBS documentary which introduced me to the subject of Chaos Theory and my first fractal I encountered in the form of the Sierpiński triangle. From that point forward into my career, I entered a world of fascination with numbers and the weird world of fractals, Chaos theory, Mandelbrot and Julia Sets and many more interesting mathematical beasts.
I happened upon that old video the other day and remembered that on the night of the broadcast of this show, I furiously scribbled down the rules for “The Chaos Game” and set about to create the Sierpinski Triangle they featured on my new Color Computer. Imagine my shock when, after about an hour of pondering and working on the code, the program ran correctly for the very first run! I was shocked and marveled that I had translated my first real world English language problem into a working algorithm!
I did take note with some sadness of seeing this video mention Prime Computer as a sponsor. I worked with Vax 11-series and Prime minicomputers for many years and it brought back a lot of cool memories of those hulking machines that were such iconic computing machines in their day.
That Color Computer is LONG gone after all these years. I have no memory of whatever happened to it but it left an indelible impression on me and I recall many happy hours of learning the basics of coding not only mathematical beasts like chaos shapes but even the fundamentals of databases by writing my own complete database system in color computer basic which stored files on 360K floppy disks. It was an ambitious effort and I was able to perfect it and use it for a number of years.

A Sierpinski Triangle, a recursive fractal shape that you can easily create with simple code.
All of that code is lost now. I was the only one to ever have seen it, but I can remember the basic bones of the database system and how it prepared me to handle my future job as a systems operator and eventually a programmer in the defense industry.
Simple systems are wonderful tools for preparing the mind for more complex endeavors and it is striking to me how many programmers now work with powerful systems and look down their nose at what we had to work with in the 1980s. There remain dedicated communities who preserve the old code and systems which run on emulators on any PC now and remain valuable tools to teach a little computing history.
Just to test my Color Computer mettle in the modern day, I decided to recreate my Sierpinski Triangle program using the VCC Color Computer Emulator. This software emulates all types of Color Computer systems and comes with built-in BASIC to allow one to run original Radio Shack software or create their own from scratch. The software is free and emulates all manner of varieties and peripherals that the COCO supported during it’s heyday.
The Sierpinski Triangle
Just to share a little about this fractal, here is the definition from Wikipedia:
“The Sierpiński triangle (sometimes spelled Sierpinski), also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.”
English Language to Code
The first step was to listen to those first moments of the PBS NOVA episode and to convert the English language explanation by Michael Barnsley of the Georgia Institute of Technology. In this short explanation by Michael, he shared the basics of the Chaos Game as follows:
- Start with a sheet of paper and create 3 points to delineate a triangle.
- Close your eyes and with a pen in hand, randomly choose a starting point and mark it on the paper.
- Now, roll a dice. In the example, Michael labeled each of the triangle vertexes with 1,2 then 3,4 and 5,6. Letting the dice roll chose a vertex. (In real code, you only use a random value of 1 to 3).
- Now here is the key to the entire algorithm: You place a mark halfway from the original starting point to the vertex of the triangle your dice roll pointed you too.
- From then on, you roll the dice and place a mark halfway from the LATEST point on the triangle and repeat the cycle. Doing this by hand on paper is sheer madness as it would take days or weeks to generate the shape that will emerge but yes, this is possible to do! It’s much better for a computer to do this for you and get a near instant result.
- Continue until the shape reaches a pleasing level of detail
Psudeocode
The resultant psudeocode is as follows:
Choose a random X and Y starting point. Mark that point.
Begin a loop having primed the algorithm with the random starting point. Two to Four thousand iterations is a good number to start with. Ten thousand iterations is a good number for a fully developed image of the triangle.
Generate a random number from 1 to 3 to accommodate the three vertexes of the triangle for both X,Y coordinates.
Halfway between the X,Y coordinates of the random “seed” starting point and the X,Y coordinates of the vertex you have chosen, mark that point using the appropriate command to light up a pixel. Insure that you set the new X and Y variable name to record the positions computed for X and Y to carry the pattern forward from the initial seed point.
Next Loop Iteration.
End
Color Computer Basic Code
It’s been 40+ years since I had written the original code, but it seemed easy enough and after studying the psuedocode I wrote, I can pleasantly share that I got things to run after about an hour of pondering what I needed to do.
The biggest problem I had to overcome was remembering the command to set a X,Y point on the screen and remembering the size of the matrix. After referring to the Color Computer Archive site , I found that the X and Y dimensions were 255 by 191 pixels. A pleasantly small playground to explore in. I wrote the following small program to insure I got the three vertexes correctly positioned:
10 PMODE 0,1
15 PCLS
20 SCREEN 1,1
25 PSET(127,0,1)
30 PSET(0,191,1)
35 PSET (255,191,1)
40 GOTO 40

The three vertexes of the triangle mapped to the proper bounds to insure we have the triangle properly mapped out.
As you can see, the vertex positions of 127,0 for the top of the triangle and 0,191 and 255,191 completed the bounds of the triangle. Realize that my selection of the graphics mode is based on “What worked for me” and doesn’t represent optimal settings.

Wacław Franciszek Sierpiński was a Polish mathematician. He was known for contributions to set theory (research on the axiom of choice and the continuum hypothesis), number theory, theory of functions and topology. He published over 700 papers and 50 books.
Hunting down Sierpinski and his Triangle
Now for the program. It did take me a bit to get out of my own way on the code. I mistakenly added new random X,Y values near line 250 and utterly destroyed the triangle until I realized my mistake and let the new computed X,Y values in the GOSUB routines do the work of carrying the “order” forward as introduced by the initial X,Y seed values in lines 220 and 230.
The Program
Feel free to scrape the program and modify, test and utterly transform it to your heart’s content. In the VCC COCO emulator, you can just paste the code directly in and type “RUN” to execute the program.
10 REM THE CHAOS GAME IN COCO BASIC BY JON ALMADA
20 REM WRITEN 12/26/21
30 REM https://afterburner1.com /2021/12/27/sierpinski-triangles-color-computers-and-clarity-of-code/
40 REM SET THE COLOR
30 C=1
100 REM INITIALIZE GRAPHICS
105 PMODE 0,1
110 PCLS
120 SCREEN 1,1
200 REM DRAW THE TRIANGLE
210 REM CHOOSE THE X,Y STARTING POINT
220 X=RND(255)
230 Y=RND(191)
240 REM LOOP THROUGH THE TRIANGLE
250 FOR L=1 to 10000
260 REM ROLL THE DICE
270 D=RND(3)
280 REM PRINT D,X,Y
290 IF D = 1 THEN GOSUB 400
300 IF D = 2 THEN GOSUB 500
310 IF D = 3 THEN GOSUB 600
320 PSET(X,Y,C)
330 NEXT L
340 GOTO 340
400 X = INT((127+X)/2)
410 Y = INT((0+Y)/2)
420 RETURN
500 X = INT((0+X)/2)
510 Y = INT((191+Y)/2)
520 RETURN
600 X = INT((255+X)/2)
610 Y = INT((191+Y)/2)
620 RETURN
Note that the graphics constraints for X,Y minimums and maximums are hard-coded into the GOSUB routines 400, 500 and 600 in the program. Optimally you would want to replace these with variables but given this was a casual thought exercise, I will leave that to you to change and explore improvements on your own initiative.
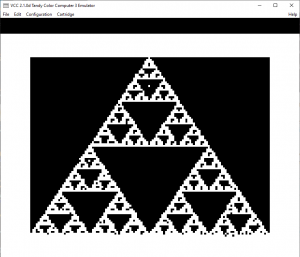
The result from my Color Computer program
Results
This is by NO means a high definition fractal program. It is a teaching tool. But the resultant display was pleasing enough to see play out much as it did on my old analog television with the Color Computer blazing along at one megahertz speed in the early 1980s.
I set this program to iterate 10,000 times to insure it properly and fully displayed the full fractal as much as possible given the constraints of the emulator and underlying graphical engine.
You are certainly encouraged to experiment with the program and set different parameters to see what it does.
Why even do this on a 40 year old computer platform?
For one, note how SIMPLE this code is. In my years in the IT world I marveled at how often programmers would obfuscate and make code so utterly complex as to be unreadable to the average person. I was lucky in life to have encountered several VERY accomplished teachers and programmers who were absolutely clear about writing easy to understand code. I made it a hallmark of my applications and earned many scowls from other programmers who did not share this philosophy, but the point is to allow others to easily grasp what you are doing and to clearly communicate ideas.
Complex Code and final thoughts
 In researching others who have done BASIC coding for the Sierpinski triangle, I did find another BASIC program that did the same thing as my program, but this one was a lot harder to figure out.
In researching others who have done BASIC coding for the Sierpinski triangle, I did find another BASIC program that did the same thing as my program, but this one was a lot harder to figure out.
Dialects of BASIC aside, there is ONLY ONE COMMENT in the aforementioned program to share with the reader what is happening. As I am not conversant with C64 BASIC, I can only guess at a lot of what is going on in this code. This is perfectly fine if you wish to just scrape code and execute the program. Not good if you want to tweak the code and experiment with it’s bounds and to see what you can push it to do.
Remember, coding is supposed to not only be optimal, but it also needs to clearly communicate what it is doing and to provide ONLY AS MUCH COMPLEXITY AS IS REQUIRED. After a certain point, too much complexity makes the code not only hard to read, but difficult or next to impossible to maintain and alter.
My own example could stand a lot more commentary but again, it was a quick and dirty effort and designed to leave it to you to carry forward and develop further or use as an inspiration.
Have fun with code! That is the best way to learn. And if you can code in old systems like the Color Computer you certainly can do so on much more advanced systems. Just remember that SIMPLE code has much to teach if you are willing to play in it’s confines. Enjoy! — Jon
:
